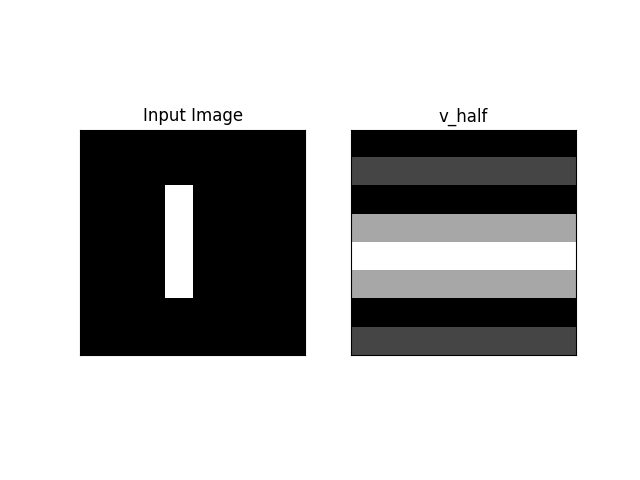Numpy 傅立葉變換 np.fft (5) 低頻的位置與原始圖像的關係
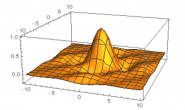
先看柱狀的原始圖
import numpy as np
import matplotlib.pyplot as plt
import src.genpic8 as pic
if __name__ == '__main__':
img = pic.backslash()
fft = np.fft.fft2(img)
amp_spectrum_nl = np.abs(np.fft.fftshift(fft))
amp_spectrum = amp_spectrum_nl
plt.subplot(121), plt.imshow(img, cmap='gray', vmin=0, vmax=255)
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122), plt.imshow(amp_spectrum, cmap='gray')
plt.title('v_half'), plt.xticks([]), plt.yticks([])
plt.show()
print('end')
運行結果如下
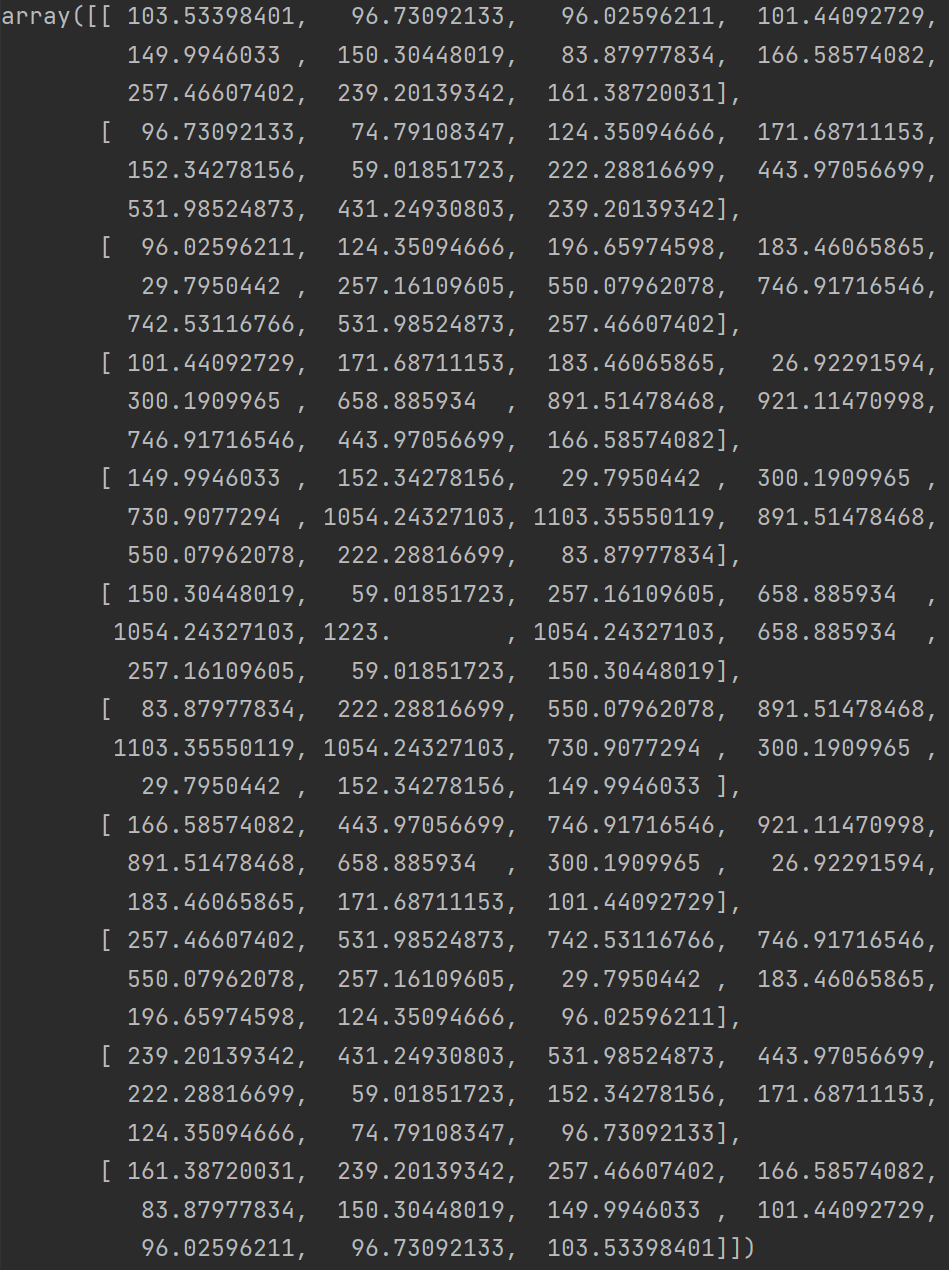
頻率數據如下
接下來是相同的原始圖片,進行旋轉
import numpy as np
import matplotlib.pyplot as plt
import src.genpic8 as pic
if __name__ == '__main__':
img = pic.pillar()
from scipy.ndimage import rotate
img = rotate(img, angle=45)
fft = np.fft.fft2(img)
amp_spectrum_nl = np.abs(np.fft.fftshift(fft))
amp_spectrum = amp_spectrum_nl
plt.subplot(121), plt.imshow(img, cmap='gray', vmin=0, vmax=255)
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122), plt.imshow(amp_spectrum, cmap='gray')
plt.title('v_half'), plt.xticks([]), plt.yticks([])
plt.show()
此處,我們使用 scipy.ndimage 來做旋轉。運行結果如下
頻率分布如下
結論
我們將原來的柱狀圖像進行旋轉後產生第二張圖。觀察到頻率分布的結果也是旋轉後的結果。經過數次的實驗測試,我們對於傅立葉變換 FT 所產生的頻率數據有更加深刻的概念,可以此為基礎進行傅立葉相關應用操作。